In 1905, Albert Einstein postulated the theory of special relativity, which expands on Newtonian mechanics to explain the motion of objects at velocities approaching the speed of light. The theory of special relativity was required to reconcile Maxwell’s Equations describing electromagnetism with Galilean Transformations describing relativistic motion according to Newtonian mechanics. Special relatively depends on two postulates: the laws of physics are the same in reference frames, and the speed of light is the same for all observers. Chief among the consequences of special relativity are the phenomena of time dilation and length contraction according to Lorentz Transforamtions. These aspects of special relativity explain the speed of light as the universal speed limit, the relativity of simultaneity, and mass-energy equivalence. Special relativity explains certain physical phenomena such as the difference in lifespan of radioactive particles traveling at high speeds compared to stationary particles, nuclear fission and fusion, and has made the Global Positioning System possible. In 1915, Einstein expanded the theory of special relativity into the theory of general relativity, which applies relativistic principles to non-inertial frames of reference not included in special relativity.
Introduction
In 1905, while working as a clerk in a Swiss patent office, Albert Einstein published his paper On the Electrodynamics of Moving Bodies, in which he postulated his theory of special relativity. ((Wikipedia, “Special Relativity,” last modified April 24, 2015, acessed May 5, 2015, http://en.wikipedia.org/wiki/Special_relativity.)) Before Einstein’s paper, scientists had struggled to explain why the theory of electromagnetism was incompatible with changing inertial reference frames. They theory of special relativity reconciled electromagnetism with Newtonian mechanics, but introduced the possibility of even more confusing phenomena.
Galilean Relativity
Contrary to popular belief, Albert Einstein was not the first physicist to propose a theory of relativity. In the seventeenth century, Galileo Galilei outlined the principles of what is known today as Galilean Relativity. ((Wikipedia, “Galilean Invariance,” last modified April 12, 2015, accessed May 3, 2015, http://en.wikipedia.org/wiki/Galilean_invariance.)) Galileo began by describing what Isaac Newton later named inertial frames of reference. An inertial frame of reference is a system of coordinates that is stationary or moving at a constant speed relative to another frame of reference. Galileo proposed that the laws of motion are the same in all inertial reference frames. ((“Galilean Relativity and Newtonian Mechanics.” Einstein Light (University of New South Wales website), n.d., accessed May 5, 2015. http://newt.phys.unsw.edu/au/einsteinlight/jw/module1_Galileo_and Newton. htm.)) For example, Galilean Relativity states that a ball dropped by a 
person sitting in a car moving at constant speed behaves according to the same laws of motion whether the motion of the ball is observed in the frame of reference of the car or the frame of reference of the Earth. However, the trajectory of the ball in each reference frame will appear differently according to each observer (Figure 1). Galileo outlined a series of transformations, known as the Galilean Transformations, which describe how the position and velocity of an object changes between different inertial reference frames based on the assumption that the time elapsed between two given events is the same in both reference frames. Just as Newtonian mechanics describes the motion of objects moving well below the speed of light with great accuracy, Galilean Transformations are very accurate at transforming object positions and velocities between inertial reference frames moving at low speed.
Problems Arise
However, in the early twentieth century, physicists began noticing discrepancies between Newtonian mechanics and Galilean Transformations, and the theory of electromagnetism proposed by James Clerk Maxwell in his 1873 paper, A Treatise on Electricity and Magnetism. Galilean Transformations and the theory of electromagnetism were found incompatible for two reasons. First, when Maxwell’s Equations, which describe electromagnetism, were subjected to Galilean Transformations, the equations yielded nonsensical results. ((Professor Mario Belloni, personal interview.)) For example, Maxwell’s Equations changed form and failed to continue to accurately describe electromagnetic behavior. The disagreements seemed to indicate that either the theory of electromagnetic behavior was wrong, or that Galilean Transformations were inadequate for electromagnetic waves. Second, Maxwell’s Equations mathematically produce a value for the speed of electromagnetic waves, more commonly referred to as the speed of light: 186,000 miles per second. At the time, it was thought that electromagnetic waves, like all other waves, require a medium through which to propagate. According to this assumptions, the movement of this peculiar medium (called the ether) through which electromagnetic waves propagate ought to affect the speed of the electromagnetic waves. However, Maxwell’s Equations gave no indication that the speed of light should change due to a change in reference frame or the motion of a medium. ((Professor John Yukich, personal interview.))
In 1887, in order to investigate whether or not the speed of light changes with the motion of the ether, physicists Albert Michaelson and Edward Morley performed an experiment at Case Western Reserve University designed to detect the motion of the ether. ((Wikipedia, “Michelson-Morley Experiment,” last modified March 8, 2015, accessed May 5, 2015. http://en.wikipedia.org/wiki/Michelson%E2%80%93Morley_experiment.)) The experiment involved firing pulses of light perpendicular to each other over the same distance and measuring 
whether one pulse of light covered the distance in less time than the other (Figure 2). A discrepancy in time elapsed would indicate that the motion of the ether had affected the speed of light that passed through it. However, in repeated trials, Michelson and Morley detected no difference in the time required for both pulses of light to cover the same distance. ((“Time Dilation and Length Contraction in Special Relativity.” Einstein Light (University of New South Wales website), n.d., accessed May 5, 2015. http://newt.phys.unsw.edu.au/einsteinlight/jw/module4_time_dilation.htm.)) The results of the Michelson-Morley experiment indicate that there is no ether, and the speed of light is invariant. Clearly, another explanation was required.
Einstein’s Solution
Einstein’s theory of special relativity is based on two postulates: 1) all the laws of physics, and not just the laws of motion, are the same in all inertial reference frames, and 2) the speed of light is the same for all observers in all reference frames. Thus, Einstein includes electromagnetism in special relativity. In order to account for light having the same speed in different reference frames, special relativity has two radical consequences: time dilation and length contraction.
The change of the amount of time elapsed between events as observed in different reference frames is called time dilation. Redefining time as a relative property of the universe rather than as an absolute property was a radical departure from Galilean relativity, and, indeed, all other previous physics. Describing the difference of position, speed, and time in different reference frames at relativistic speeds requires a different set of transformations, called the Lorentz Transformations. Recall that the assumption in the Galilean Transformations that the time elapsed between events is constant in different reference frames requires changes in position and velocity of objects between inertial reference frames. By the same principle, keeping the velocity of light constant between inertial reference frames for the Lorentz transformations requires a change in position and time.
To understand how time dilation works, imagine a spaceship flying at a constant speed and equipped with a light generator, light detector, and a mirror (Figure 3). An astronaut inside the spaceship measures that the light takes a certain amount of time to propagate out from the emitter, reflect from the mirror, and return to the detector. However, to an observer outside the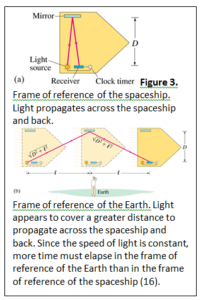 
spaceship on Earth, the light appears to follow a longer, diagonal path to reflect from the mirror and return to the detector. Since the light must move at the same speed, the amount of time required for the light to cover that distance must be longer. Thus, the observer on Earth experiences more time than the astronaut inside the spaceship. The shortest time elapsed, called proper time, will always be measure in the frame of reference of the observer who measures both events (the light propagating out and returning) in the same location. In the example of the spaceship, the astronaut in the spaceship measures the proper time, and the observer on Earth experiences dilated time.
Length contraction is another consequence of special relativity. It is the shortening of the length of high-speed objects in the direction those objects are traveling as observed from a stationary frame of reference. If observers in different reference frames agree on velocity but disagree on time elapsed, by necessity they must disagree on length as well in order to agree on the same law of physics. The disagreement about time causes observers in any frame of reference to measure lengths moving in other frames of reference as shorter than they really are. However, lengths are only contracted in the direction of the motion of the object. The longest length (the proper length) is measured in a frame of reference in which the object is stationary. In the example of the spaceship, the astronaut observes the proper length of the spaceship. The observer on Earth measure the length of the spaceship contracted. However, the observer on Earth measures the proper length of the distance the spaceship travels, and the astronaut measures a contracted distance traveled.
It is important to note that time dilation and length contraction are only significant effects for objects and frames of reference moving at velocities nearing the speed of light. For example, an object traveling at 10% the speed of light only has its length contracted by 0.5%. ((“Length Contraction,” The Physics Classroom, n.d., accessed May 5, 2015, http://www.physicsclassroom/com/nmedia/specrel/lc.cfm.)) A velocity of 10% of the speed of light is typically considered the threshold at which relativistic effects must be considered. However, 10% the speed of light is 18,600 miles per second. Thus, while time dilation and length contraction are experimentally verified effects and do occur for all motion, those effects can be ignored in ordinary circumstances.
Implied Phenomena
Special relativity implies the possibility of a series of baffling phenomena concerning the behavior of objects moving at velocities nearing the speed of light. Chief among these phenomena are the relativity of simultaneity, mass-energy equivalency, and the universal speed limit.
Events are simultaneous if they occur at the same time. However, time dilation between reference frames leads to the conclusion that events that are simultaneous in one frame of reference may not be simultaneous in another frame of reference. Thus, the theory of special relativity casts simultaneity as a relative phenomenon rather than an absolute one, as the theory does with all time-dependent phenomena. The relativity of simultaneity can lead to some puzzling apparent paradoxes, the most famous being the barn-pole paradox (Figure 4).
Imagine a barn with doors at both ends which rapidly open and close at the same time. Now, consider a pole that is about twice the length of the barn. The pole is traveling near the speed of light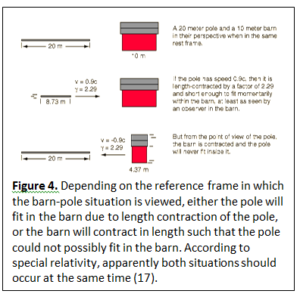
through the barn such that due to length contraction, there is an instant in which both barn doors can close and the pole is enclosed in the barn. From the frame of reference of the barn, the pole will fit perfectly in the barn before the doors reopen and the pole flies off. However, in the frame of reference of the pole, the barn appears to approach the pole at the speed of light. Thus the barn will contract in length so that the pole is longer than the barn and both barn doors can’t close around the pole at the same time. ((Robert Firth, Philip Gibbs, and Scott Chase, “A Special Relativity Paradox: The Barn and the Pole,” The Physics and Relativity FAQ (University of California-Riverside Department of Mathematics website), 1997, accessed May 5, 2015, http://math.ucr.edu/home/baez/physics/Relativity/SR/barn_pole.html.)) According to special relativity, both of these outcomes should occur at the same time!
The resolution of this apparent paradox lies in the relativity of simultaneity. While both doors close simultaneously in the barn’s frame of reference, they close at different times in the pole’s frame of reference. First, the far door will close as the pole flies into the barn. Then, the far door will reopen and the pole will begin to pass out of the barn. As the back edge of the pole enters the barn, the near door will close and reopen behind the pole, and the pole will fly out of the barn unhindered.
Another phenomena implied by special relativity is mass-energy equivalence.
